Таблица Неопределенных Интегралов Шпаргалка
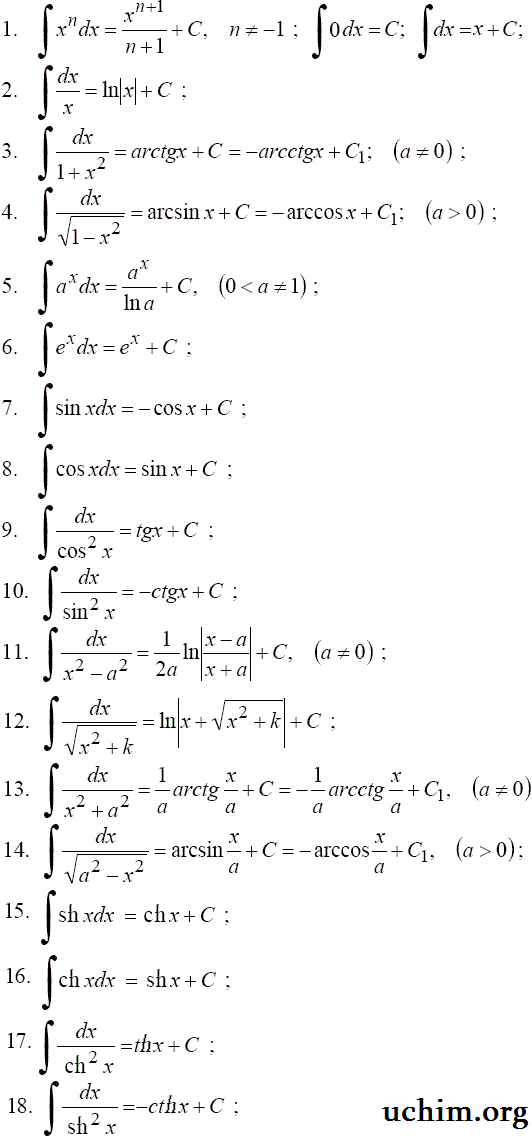
Непосредственное интегрирование базируется на использовании свойств неопределенных интегралов,, правила интегрирования и таблицы первообразных. Обычно, подынтегральное выражение сначала требуется слегка преобразовать, чтобы можно было использовать таблицу основных интегралов и свойства интегралов. Найти интеграл. Коэффициент 3 можно вынести из-под знака интеграла на основании свойства: Преобразуем подынтегральную функцию (по формулам тригонометрии): Так как интеграл суммы равен сумме интегралов,. Пришло время обратиться к таблице первообразных: Ответ.
Обращаемся к таблице первообразных для показательной функции:. Если использовать правило интегрирования, то имеем: Таким образом, таблица первообразных вместе со свойствами и правилом интегрирования позволяют найти массу неопределенных интегралов. Однако, далеко не всегда можно преобразовать подынтегральную функцию, чтобы использовать таблицу первообразных. К примеру, в таблице первообразных отсутствует интеграл от функции логарифма, функции арксинуса, арккосинуса, арктангенса и арккотангенса, функции тангенса и котангенса. Для их нахождения применяются специальные методы.
Таблица Интегралов И Производных

- Таблица неопределенных. Можно скачать таблицу неопределенных интегралов.
- Таблица неопределённых интегралов. Правила интегрирования.

Табличные Интегралы
Но об этом в следующем разделе:. Некогда разбираться?